Swim in rising water - Dijsktra optimization

 Problem statement:

You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j).

The rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.

Return the least time until you can reach the bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).

 

ELI5: 

Find the shortest path between [0,0] to [n-1, n-1]. i must admit i thought this was some kind of a backtracking problem

Rant

The description is garbage

At time t, the depth of the water everywhere is t. WTF its supposed to mean ?

What the problem is about:

 

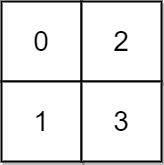
we just need to find the path from (0,0) to (1,1) with very less time, lets go through all the shortest paths

 

 

 In the testcase it doesnt really matter about which path we take because (n-1, n-1) has highest value 3 so we would have to wait 3 to swim to (n-1, n-1), but lets consider the other example

 

 

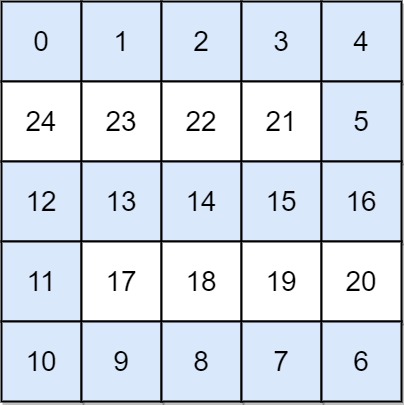
Here if we hadnt chose this path then would have run in to 24, 23 which are high than the highest value in this path ( 16 )

 

But how do we find such path ? 

By bruteforcing ofcourse :-), but bruteforcing is not very efficient, you can find the reason here. Instead of bruteforcing we directly get started with dijsktra. Staring from 0,0 we get all adjacent cells and put them to min heap. Now in our heap grid with min value would be chosen for iteration. Then we repeat the same procedure. By being greedy with our choice to choose the cells with least value we will surely avoid a lot of iterations.

class Solution:

def swimInWater(self, grid: List[List[int]]) -> int:

ROWS, COLS = len(grid), len(grid[0])

min_heap = [[grid[0][0], 0, 0]]

max_val = grid[0][0]

directions = [[0,1], [1,0], [0,-1], [-1,0]]

visited = set()

while min_heap:

val, r, c = min_heap.pop()

max_val = max(val, max_val)

if r == ROWS - 1 and c == COLS-1:

break

for dx, dy in directions:

tx, ty = r+dx, c+dy

if 0 <= tx < ROWS and 0 <= ty < COLS and (tx,ty) not in visited:

heapq.heappush(min_heap, [grid[tx][ty], tx, ty])

visited.add((tx,ty))

return max_val

here we partially applied dijsktra though, i dont feel like its dijsktra though because in dijsktra our major objective is to prevent recomputing distance after we discover a new shortest path. Here there is no computations relative to the path, but instead we choose the cell greedily to avoid walking in to cell with max value